TIPOS DE ESTIMACIÓN Y CARACTERÍSTICAS

       QUE ES UNA ESTIMACIÓN EN ESTADÍSTICA?

Una estimación estadística es un proceso mediante el que establece que valor debe tener un parámetro según deducciones que realizamos a partir de estadísticas. 

En otras palabras, estimar es establecer conclusiones sobre características poblacionales a partir de resultados muéstrales.

ESTIMACIÓN

Estimar qué va a ocurrir respecto a algo (o qué está ocurriendo, o qué ocurrió), a pesar de ser un elemento muy claramente estadístico, está muy enraizado en nuestra cotidianidad. Dentro de ello, además hacemos estimaciones dentro de un intervalo de posibilidades. 

• Por ejemplo: “creo que terminaré la tarea en unos 5-6 días”. Lo que hacemos en el terreno del análisis de datos es aplicar matizaciones técnicas a este hábito. Vamos a dedicar este documento al concepto de estimación, comenzando con la estimación puntual. Después nos ocuparemos de desarrollar un modelo de estimación por intervalo donde identificaremos los elementos fundamentales, con su significado y símbolo. Y, por último, habrá que desarrollar cómo se calculan esos elementos.

Existen algunos tipos de estimación estadística.

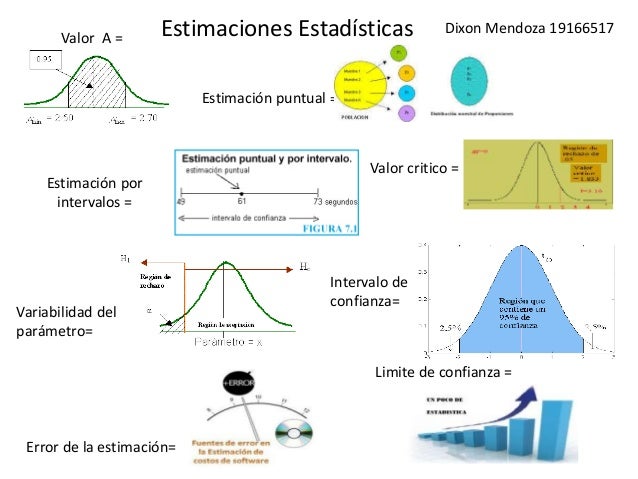
a)      Estimación Puntual 

Una estimación es puntual cuando se usa un solo valor extraído de la muestra para estimar el parámetro desconocido de la población. Al valor usado se le llama estimador.

Aunque es una forma muy común para expresar las estimulaciones deja espacio para muchas otras preguntas, por  ejemplo, no nos dice de cuanta información se basa la estimulación,  ni nos dice nada sobre el tamaño de la muestra y el tamaño posible del error. Así tal vez se tendría que completar  un estimulador punto A con el tamaño de una muestra y el valor de var (θ) o con alguna otra información.

     Muestral del estimulador puntual, una de las formas es:

p(θ^∆,<θ<θ^∆ )=1-∝

Donde Z, acento circunflejo son valores enfocados de teta de acento circunflejo y  lo cual es igual: 1-∝

Para una probabilidad especifica de un numero alfa nos referimos aθ^∆,θ<θ₂Confianza (1-∝) 100% para teta.

También 1-∝ se llama grado de confianza y los puntos terminales del intervalo se llaman límites de confianza interior y superior.

Por ejemplo cuando ∝=0.05 el grado de confianza es  0.95 por lo que tenemos un valor de confianza de 95%. Los estimadores de intervalo de un parámetro dado no son únicos.

P (〖 θ〗^∆,θ<θ_2) = 1-∝ =1-∝  grado de confianza

            = (1-∝) 100% intervalo de confianza

∝=0.05

Grado de confianza -0.95

Intervalo “95%”

b)   Estimación por Intervalo

Una estimación por intervalo de un parámetro θ es algún par de funciones de la muestra que satisfacen L(x) ≤ U(x) para todo x ∈ X . El intervalo aleatorio [L(X), U(X)] es llamado un estimador por intervalo.

 EJEMPLO: Si se dice que una distancia viene dada por 5.28 pies, se está dando una estima de punto. Si, por otra parte, se dice que la distancia es 5,28 +- 0.03 pies, es decir, la distancia real se encuentra entre 5.25 y 5.31 pies, se está dando una estima de intervalo,

     La precisión o conocimiento del error de una estima se conoce también como su seguridad.

     Dos problemas de diferencia estadística se dividen es problemas de estimación y pruebas  de hipótesis aunque en realidad son dos problemas de decisión y por lo tanto no se pueden manejar con un enfoque limitado.

     La diferencia principal entre las dos clases de problemas es que los problemas de estimación debemos determinar el valor de un parámetro o los valores de varios parámetros de un continuo posible de alternativas mientras que en las pruebas de hipótesis debemos de medir   si aceptamos o rechazamos un valor especifico o un conjunto de valores específicos de un parámetro.

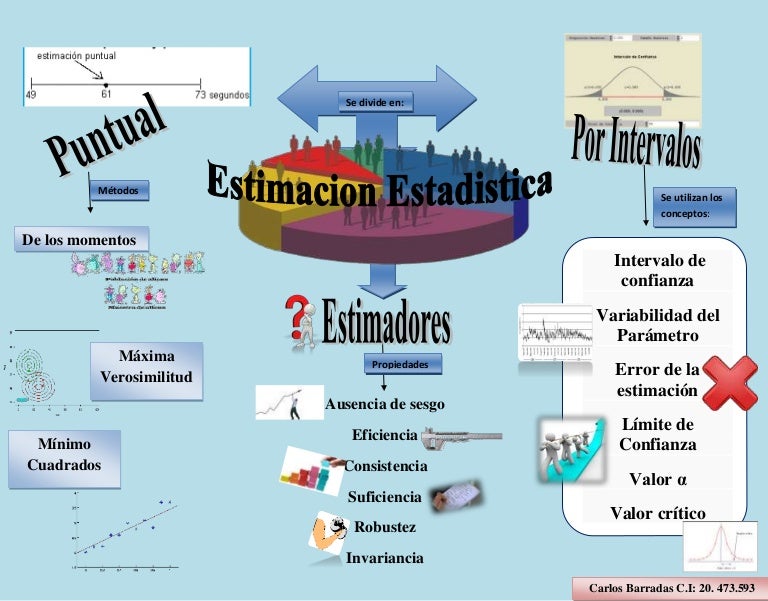
     La estimación de un parámetro involucra el uso de los datos muéstrales en conjunción con alguna estadística. Existen dos formas de llevar a cabo la anterior estimulación puntual o intervalo.

     En la primera se busca que con base a los datos muéstrales de origen  a una estimulación evaluada del parámetro y que recibe el nombre de estimador puntual. Para la segunda se determina un intervalo en la que forma probable se encuentre el valor de parámetro y recibe el nombre de intervalo de confianza.

• EN LA ESTIMACION SE UTILIZAN LOS SIGUIENTES CONCEPTOS

INTERVALO DE CONFIANZA

El intervalo de confianza es una expresión del tipo [θ₁, θ₂] ó θ₁ ≤ θ ≤ θ₂, donde θ es el parámetro a estimar. Este intervalo contiene al parámetro estimado con un determinado nivel de confianza. Pero a veces puede cambiar este intervalo cuando la muestra no garantiza un axioma o un equivalente circunstancial.

VARIABILIDAD DE PARÁMETRO

Si no se conoce, puede obtenerse una aproximación en los datos aportados por la literatura científica o en un estudio piloto. También hay métodos para calcular el tamaño de la muestra que prescinden de este aspecto. Habitualmente se usa como medida de esta variabilidad la desviación poblacional y se denota σ.

ERROR DE LA ESTIMACIÓN

Es una medida de su precisión que se corresponde con la amplitud del intervalo de confianza. Cuanta más precisión se desee en la estimación de un parámetro, más estrecho deberá ser el intervalo de confianza y, si se quiere mantener o disminuir el error, más observaciones deberán incluirse en la muestra estudiada. En caso de no incluir nuevas observaciones para la muestra, más error se comete al aumentar la precisión. Se suele llamar E, según la fórmula E = (θ₂ - θ₁)/2.

c) Estimación Sesgo

 Se denomina sesgo de un estimador a la diferencia entre la esperanza (valor esperado) del estimador y el verdadero valor del parámetro a estimar. Es deseable que un estimador sea insesgado o centrado, esto es, que el sesgo sea nulo para que la esperanza del estimador sea igual al valor del parámetro que se desea estimar.

                   

CARACTERÍSTICAS QUE DEBE TENER UN BUEN ESTIMADOR

 1. Debe ser insesgado: un estimador es insesgado, si en promedio, tiende a tomar valores que están por encima del parámetro de la población con la misma frecuencia y la misma extensión, con la que tiende a asumir valores por debajo del parámetro de población que se está estimando.

 2. Debe ser eficiente: de varios estimadores insesgados, el más eficiente es el que tiene el error estándar más pequeño.

3. Debe ser consistente: significa que a medida que aumenta el tamaño de la muestra, la estimación se aproxima al valor del parámetro.

4. Debe ser suficiente: significa que ningún otro estimador puede suministrar más información sobre el parámetro.